Okręgowa Komisja egzaminacyjna w Krakowie
O podręczniku matematyki
(Z podziękowaniami dla Stefana Turnaua)
1. Przygoda z podręcznikiem
Zespołowa praca nad podręcznikiem matematyki może mieć charakter intelektualnej
przygody. Dużo zależy od osoby kierującej zespołem, która powinna stworzyć twórczą, otwartą,
partnerską atmosferę - dotyczy to zwłaszcza sytuacji, gdy członkowie zespołu mają różny
poziom doświadczenia życiowego i zawodowego. Nasza przygoda z podręcznikiem matematyki
(piszę te słowa także w imieniu Marii Legutko) rozpoczęła się w lipcu 1975 roku podczas
przypadkowego spotkania ze Stefanem Turnauem (i jego synami Marcinem i Grzegorzem)
na drodze do Morskiego Oka. Zaczęliśmy rozmawiać o matematyce i jej nauczaniu.
Rozmawialiśmy dalej w czasie wspinania się drogą na Szpiglasową Przełęcz,
rozmowy nie zakończyliśmy nawet nad Doliną Pięciu Stawów.
Ta podróż sprzed lat, wspinaczka, wysiłek i trud ale także satysfakcja, głębokie doznania,
obcowanie z potęgą i pięknem, jest dla nas wciąż metaforą wspólnej intelektualnej przygody
podczas prac nad podręcznikami matematyki.
2. Z podręcznikiem w czas reform
Przez ostatnie ćwierć wieku podejmowano w Polsce mniej lub bardziej intensywnie próby
reformy nauczania matematyki. Stefan Turnau nigdy nie był obojętny wobec prac reformatorów,
pełniąc często rolę, którą dziś w literaturze zachodniej określa się mianem "critical friend". Jego
wystąpienia, zawsze znaczące, pełne były pasji i zaangażowania, krytycyzmowi towarzyszyły
jednak zawsze propozycje czy sugestie kierunku prac nad ulepszeniem nauczania matematyki.
Świadectwa tej drogi postępowania można znaleźć w pracy habilitacyjnej Stefana Turnaua, "Rola
podręcznika szkolnego w kształceniu pojęć i rozumowań matematycznych na poziomie pierwszej
klasy ponadpoczątkowej" (1978). We wstępie czytamy:
3. Rady dla autorów podręczników matematyki
Warto przypomnieć konkluzje pracy habilitacyjnej Stefana Turnaua (obudowane tam
wieloma przykładami i szeroko omówione), które nadal mogą znaleźć się w nieopublikowanym
jeszcze przewodniku dla autora podręcznika matematyki.
Stefan Turnau i kierowane przez niego zespoły autorów podręczników starali się stosować
powyższe rady w praktyce. Poniższy przykład pochodzi z podręcznika matematyki do klasy IV.
4. Przykład
Uczeń może przeczytać co Tomek odpowiedział i co zapisał na tablicy:
Tomek popełnił błąd, na co od razu reaguje Agnieszka:
Do dyskusji włącza się Dyzio, ostatnie słowo należy jednak do Agnieszki:
Czy taka rozmowa rzeczywiście miała miejsce? To nie ma znaczenia. W koncepcji dydaktycznej
nauczania matematyki Stafana Turnaua powinno znaleźć się miejsce w klasie na takie rozmowy.
Tomkowi przydarzył się błąd, który profesor Anna Krygowska nazwałaby "błogosławionym
błędem" i który można - jak pokazano w podręczniku - wykorzystać dla pojęciowego
wprowadzenia prawa łączności mnożenia.
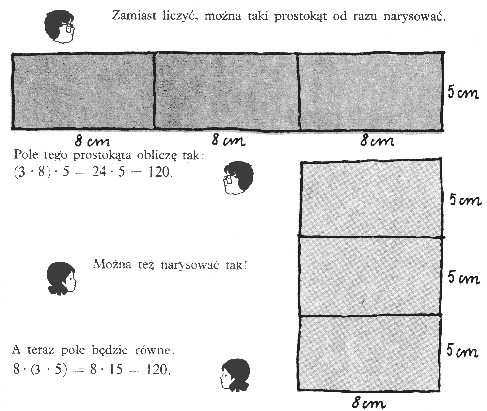
Rozmowa miała dalszy ciąg: Tomek i Dyzio czynnościowo opisali łączność mnożenia:
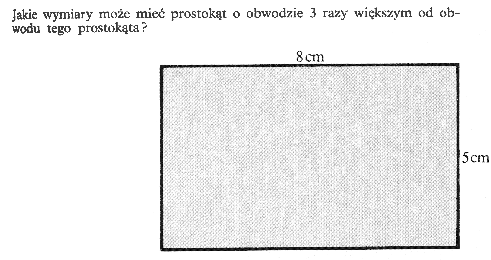
Nasępnie pojawia się przykład poprawnego zastosowania
pomysłu Tomka powiększania obu boków prostokąta w powiększaniu obwodu
prostokąta.
Na końcu pojawiają się przykłady zastosowania prawa łączności.
5. Czy szkoła jest krainą marzeń?
W podręczniku matematyki dla klasy IV jedną z głównych ról odgrywał Dyzio. Kto był
pierwowzorem tej postaci, skąd pomysł takiego właśnie imienia? Możemy snuć różne domysły.
W zasobach Internetu imię Dyzio związane jest przede wszystkim z wierszem Juliana Tuwima
"Dyzio Marzyciel", który marzył leżąc na łące o obłoczkach ze słodkiego kremu. Jolanta
Paczkowska proponuje na jednej ze stron w Internecie, by wiersz ten, wraz z wierszem Joanny
Kulmowej "Marzenia" wykorzystać na lekcji o szkole jako krainie marzeń. Przesłanie tej lekcji
nie jest optymistyczne. Dzieci mają zapisać na tablicy, że
Szkoła nie powinna kojarzyć się z marzeniami, które w tym miejscu rozwiewają się, uciekają.
Dyzio Stefana Turnaua ma odwagę marzyć nie tylko o obłoczkach ze słodkiego kremu.
Ze swadą, dużą swobodą, inteligencją i zdrowym rozsądkiem mierzy się z wyzwaniami
matematyki w szkole. Wraz ze Stefanem Turnauem marzymy o dobrym podręczniku matematyki
w szkole. Marzenia towarzyszą nam w górach, w domu i w szkole. I za to dziękujemy Stefanowi.
- uwzględniać obserwowane u niektórych uczniów zainteresowanie sytuacjami czysto
abstrakcyjnymi (wbrew poglądowi, że dzieci interesują się tylko zagadnieniami
praktycznymi),
- obejmować gry, zabawy i łamigłówki, wykorzystując występujące często u dzieci
predylekcję do tego typu aktywności umysłowej,
- korzystać z występującego u wielu dzieci poczucia zadowolenia estetycznego wobec
przejawów regularności w samej matematyce lub graficznych sposobach jej wyrażania.


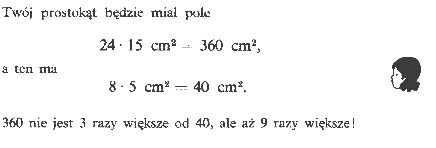

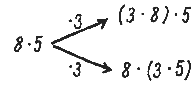
W SZKOLE: W DOMU:
- nie ma marzeń - są marzenia
- ani w tornistrze - pod stołem
- ani pod ławą - w jakieś szparze