Stefan Turnau
O dowodzeniu twierdzeń we współczesnej szkole
Matematyka była i jest przedstawiana w szkole jako domena absolutnych prawd i
niezawodnych algorytmów, których doskonałość zawdzięczamy żelaznej logice dowodów.
Toteż śledzenie i uczenie się gotowych dowodów oraz rozwiązywanie zadań "na
dowodzenie" stanowiły istotny składnik programu nauczania. Nie zapomnijmy też, że dowód
był jednym z etapów rozwiązania zadania konstrukcyjnego, jakich obfitość zwierały
podręczniki. Była to - jak utrzymywały cele kształcenia - nauka rozumowania dedukcyjnego,
najważniejszy cel nauczania geometrii, a może w ogóle matematyki.
Tak było mniej więcej do roku 1980. Czasy teraz mamy inne. Dowody pojawiają się
na lekcjach rzadko (jeżeli w ogóle), bo i czasu na matematykę o wiele mniej, i nauka
rozumowania dedukcyjnego zeszła w celach kształcenia nieomal poza horyzont. Matematyka
szkolna - wbrew hasłom sprzed półwiecza - oddaliła się od akademickiej bardziej niż
kiedykolwiek. Nie tylko jej treść i ujęcie są anachroniczne; zaciera się to, co w matematyce
zdaje się najistotniejsze: abstrakcyjność i dedukcyjność. Czy to dobrze? Czy tak być musi?
Czy ten trend chcemy odwrócić? Czy da się to zrobić? Jak?
Uniwersytet Rzeszowski
(rozszerzony tekst wystąpienia)
Zacznijmy od przyjrzenia się statusowi dowodu w matematyce. Ludzie spoza świata matematyki, w tym uczniowie, na ogół nie wiedzą, że wśród dowodów produkowanych przez matematyków roi się od takich, które dowodami nie są, bo zawierają lukę, pominięcie przypadku, błędne koło, a bywa, że i błąd rachunkowy. I wcale nie kompromituje to autorów; przeciwnie, te błędne dowody często istotnie przyczyniły się do rozwoju matematyki (np. liczne "dowody" piątego postulatu Euklidesa). Man Keung Siu [Man Keung Siu, Mathematiques = Démonstration?, APMEP, Bulletin 434, 2001. Z tego artykułu zaczerpnąłem też niektóre inne informacje.] w artykule pt. "Czy matematyka = dowód?" przypomina takie oto fakty.
Słynny problem czterech kolorów (sformułowany w roku 1852) "rozwiązał" w 1879 adwokat angielski Kempe, a dopiero jedenaście lat później matematyk angielski Heawood pokazał, że rozwiązanie jest błędne. Jednak pomysł Kempego stał się podstawą dalszych badań, które przyniosły ostateczne rozwiązanie w roku 1976, po\ldots 1200 godzinach pracy komputera; ale czy można to uznać za dowód? Błędne dowody trafiały (a może trafiają?) się w podręcznikach szkolnych. Przypomnę, że zaproponowany przez Legendre'a "dowód" piątego postulatu Euklidesa - jeden z wielu pozornych dowodów tego faktu - przez lat dwadzieścia powtarzano w podręczniku tego autora (tłumaczonego także na polski) i innych. Ilu uczniów w XIX-wiecznej Europie musiało się go nauczyć? Czy ponieśli przez to szkodę, czy może raczej odnieśli korzyść, ucząc się tego krótkiego i eleganckiego rozumowania?
Oto inny przykład. Rysunek 1, ilustrujący zamianę równoległoboku na prostokąt o tym samym polu P, boku a i wysokości h, nie jest - z czego nawet wielu nauczycieli nie zdaje sobie sprawy - dowodem wzoru P = ah, bo tak nie da się zamienić na prostokąt o boku a równoległoboku na rysunku 2.
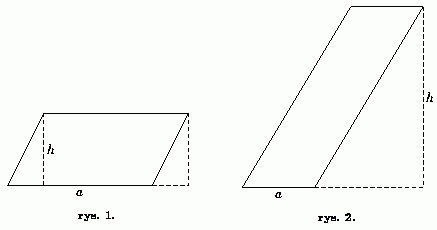
Dowód w przypadku ogólnym jest trudniejszy i z pewnością nie mógłby znaleźć się w programie szkoły podstawowej. Jaki jest więc status tej pokazywanej uczniom konstrukcji, której matematyczna uczciwość nie pozwala nazwać dowodem? Odpowiedź na to pytanie jest tym ważniejsza, że przykładów ułomnej argumentacji na użytek szkolny jest wiele.
Dowodom nie można więc ufać baz zastrzeżeń. A z drugiej strony - jakże często uznajemy prawdziwość faktów, których dowodu nie znamy, i to wcale nie dlatego, że stoją za nimi autorytety. Dwie wysokości trójkąta przecinają się, prawda? Nikt nie pyta o dowód takiej oczywistości. Trzy wysokości trójkąta przecinają się w jednym punkcie, prawda? Dla nauczyciela to już nie oczywistość, a dla ucznia? Uczył się wykreślania wysokości, symetralnych boków i dwusiecznych kątów na długo zanim mógłby zrozumieć, na czym tu polega problem. Widział zawsze trzy proste przechodzące przez wspólny punkt; czy może w to wątpić? Nie dajemy mu okazji do takiego wątpienia, sprawdzania, szukania przyczyny, więc wierzy w to, co widzi. I nie ma w tym niczego zdrożnego. Bądźmy tego świadomi i nie udawajmy, że ucznia przekonaliśmy dowodem.
Bywa też inaczej: trudno uwierzyć w fakt udowodniony, nawet po zapoznaniu się z dowodem.
Dowód nie zawsze więc przekonuje.
Za to jak silnie przekonujące bywają rozumowania nie w pełni
ścisłe! W trzecim
wieku przed Chrystusem Archimedes znalazł i udowodnił wzór na pole
elipsy 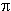 ab, gdzie a, b
są długościami półosi. Kładąc a = b = r,
otrzymujemy wzór na pole koła
o promieniu r:
ab, gdzie a, b
są długościami półosi. Kładąc a = b = r,
otrzymujemy wzór na pole koła
o promieniu r: 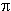 r2.
Stosunek pola koła do pola opisanego na nim kwadratu wynosi
r2.
Stosunek pola koła do pola opisanego na nim kwadratu wynosi 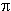 /4.
Taki sam jest stosunek
obwodu koła do obwodu kwadratu opisanego. Wreszcie tę samą liczbę
/4.
Taki sam jest stosunek
obwodu koła do obwodu kwadratu opisanego. Wreszcie tę samą liczbę
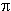 /4 otrzymujemy jako stosunek pola elipsy do pola
opisanego na niej prostokąta. Trudno oprzeć się przypuszczeniu,
że i stosunek obwodu elipsy do obwodu opisanego prostokąta wyniesie
/4 otrzymujemy jako stosunek pola elipsy do pola
opisanego na niej prostokąta. Trudno oprzeć się przypuszczeniu,
że i stosunek obwodu elipsy do obwodu opisanego prostokąta wyniesie
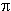 /4, a stąd wzór na
obwód elipsy
/4, a stąd wzór na
obwód elipsy 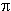 (a + b). Taki właśnie wzór na długość
elipsy podał w
XIII wieku Fibonacci (może tak właśnie rozumując) i przez ponad pięć
stuleci nie wiedziano, że jest on błędny.
Dopiero w XIX wieku, dzięki rachunkowi całkowemu, można było nie tylko to udowodnić,
ale też pokazać, że wzór na długość elipsy w ogóle nie jest funkcją elementarną długości jej
półosi, a więc nie istnieje dla niej żaden wzór. O ile tymczasem wzoru używano (do czego?) -
otrzymywano wystarczająco dokładny wynik. Obliczmy bowiem w przybliżeniu długość
elipsy jako pole paska o tej właśnie długości a szerokości 1 (odejmując pola dwóch elips), a
potem zróbmy to samo dla okręgu. Okaże się, że wzór daje przybliżenie długości elipsy z
bardzo dużą dokładnością.
(a + b). Taki właśnie wzór na długość
elipsy podał w
XIII wieku Fibonacci (może tak właśnie rozumując) i przez ponad pięć
stuleci nie wiedziano, że jest on błędny.
Dopiero w XIX wieku, dzięki rachunkowi całkowemu, można było nie tylko to udowodnić,
ale też pokazać, że wzór na długość elipsy w ogóle nie jest funkcją elementarną długości jej
półosi, a więc nie istnieje dla niej żaden wzór. O ile tymczasem wzoru używano (do czego?) -
otrzymywano wystarczająco dokładny wynik. Obliczmy bowiem w przybliżeniu długość
elipsy jako pole paska o tej właśnie długości a szerokości 1 (odejmując pola dwóch elips), a
potem zróbmy to samo dla okręgu. Okaże się, że wzór daje przybliżenie długości elipsy z
bardzo dużą dokładnością.
Wiemy, jak Euler znalazł sumę szeregu
1 + (1/2)2 + (1/3)2 + (1/4)2+ ...
bo to opisał. Wyszedł od równości
sinx = x - x3/(3!) + x5/(5!) + ... ,
co po podzieleniu obustronnie przez x daje
sinx/x = 1- x2/(3!) + x4/(5!) - ... (*)
Prawa strona bardzo przypomina wielomian, a przy tym ma nieskończenie wiele miejsc zerowych, co sugeruje analogię z wielomianem o n miejscach zerowych
a0 + a1x + a2x2 + ... + anxn.
Rozkłada się on na czynniki
an(x - a1)(x - a2)...(x- an),
gdzie ai oznaczają miejsca zerowe, co można przekształcić do postaci
a0(1 - x/a1) (1 - x/a2)... (1 - x/an).
W przypadku podobnego do (*) wielomianu
b0 - b1x2 + b2x4 - ... + bnx2n
o miejscach zerowych  1,
-
1,
-  1,
1,
 2,
-
2,
-  2
...
2
...
 n,
-
n,
-  n,
rozkład ten redukuje się do
n,
rozkład ten redukuje się do
b0(1 -
x2/ 12)
(1 - x2/
12)
(1 - x2/ 22)
...
(1 - x2/
22)
...
(1 - x2/ n2).
n2).
Porównując współczynniki przy x2 otrzymamy
b1 = 1/ 12
+ 1/
12
+ 1/ 22 + ... +
1/
22 + ... +
1/ n2.
n2.
Ponieważ zaś miejsca zerowe funkcji (*) to liczby
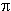 , -
, - 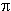 ,
2
,
2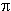 , -2
, -2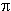 ,
3
,
3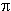 , ... więc przez analogię
, ... więc przez analogię
1/2  3 = 1/
3 = 1/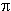 2 +
1/(4
2 +
1/(4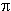 2) + 1/(9
2) + 1/(9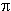 2) +
... ,
2) +
... ,
skąd
1 + 1/4 + 1/9 + ... = 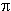 2/6.
2/6.
Euler oczywiście wiedział, że to nie dowód (dowód znalazł dopiero dziesięć lat później), jednak wynik uważał za poprawny.
Potoczne wyobrażenie o matematycznym dowodzie jako konstrukcji skończonej i doskonałej, będącej błyskiem geniuszu, nie odpowiada codziennej matematycznej rzeczywistości. Matematycy to wszak ludzie, dowodzenie jest działalnością ludzką, a więc nosi wszelkie jej cechy. Nic nie wiemy na ogół o wczesnych zawiązkach idei dowodu, rodzącej się w umyśle matematyka i dojrzewającej stopniowo, a potem mozolnie wypełnianej szczegółami; o niezliczonych zahamowaniach, wątpliwościach i potknięciach w toku tej roboty; o błędach odkrywanych wtedy, gdy cel wydał się ostatecznie osiągnięty; o pomysłach porzuconych - choć takie piękne - bo nie dały się zrealizować. Studiując dowód - produkt tej pracy, niekiedy rzeczywiście godzien podziwu i cieszący specyficzną urodą, nie myślimy o tym, że powstawał długo i w bólach. Niewyobrażalne wydaje się samodzielne wymyślenie podobnego. A przecież nawet te już gotowe dowody nierzadko okazują się błędne. Według jednego z redaktorów prestiżowego pisma Mathematical Review, niemal połowa opublikowanych tam dowodów zawiera błędy, choć twierdzenia są w większości prawdziwe. Pamiętajmy zatem: Nie od razu Kraków zbudowano i Nie święci garnki lepią.
Naukę dedukcji zacząć trzeba od rzeczy zdawałoby się banalnej: nie zawsze uczeń odróżnia wysłowienie faktu od argumentu na rzecz jego prawdziwości. Przyzwyczajony odpowiadać prawie zawsze na pytanie JAK JEST, tak samo odpowiada na nieoczekiwanie zadane mu pytanie PRZEKONAJ MNIE, ŻE TAK JEST. Ile wynosi 6 razy 7? 42. Przekonaj mnie, że tyle. Bo jak pomnożymy 6 przez 7, otrzymamy 42. Gdyby uczeń miał świadomość, że na to pytanie trzeba co najmniej przytoczyć inny fakt, a nie wystarczy zmienić wysłowienie tego, którego dotyczy pytanie, mógłby odpowiedzieć "Bo 6 razy 6 jest 36 i jeszcze 6 to 42" albo "Bo to tyle samo co 7 razy 6" czy też "Bo to musi być w środku między 36 i 49" itp. Bez tej świadomości nie można zrozumieć, czym jest wynikanie.
Wynikanie to związek dwóch faktów. Taki mianowicie, że ilekroć zachodzi pierwszy - koniecznie musi zajść i drugi. Stąd, że liczba jest podzielna przez 2 wynika, że jej kwadrat jest podzielny przez 4. Mniejsza o to, skąd to wiadomo; ważne jest, co to znaczy. A zrozumieć, co to znaczy, nie można bez zrozumienia, co znaczy "nie wynika". Stąd, że suma dwóch liczb jest podzielna przez n nie wynika, że składniki są podzielne przez n. Nie wynika, bo chociaż suma 7+5 jest podzielna przez 3, 7 ani 5 nie są podzielne przez 3. Rozumienie wynikania musi też obejmować świadomość, że jest to relacja niesymetryczna: choć z A wynika B, niekoniecznie z B wynika A. Stąd, że dwie figury są przystające, wynika, że mają równe pola; ale stąd, że mają równe pola nie wynika ich przystawanie. Rozumienie przez ucznia wynikania (i niewynikania) można ocenić po sposobie konstruowania przez niego przykładów sprawdzających. Czy stąd, że w czworokącie przekątne są prostopadłe, wynika, że jest to romb? Uczeń nie w pełni rozumiejący wynikanie, a więc i pytanie, dla sprawdzenia rysuje romb, a następnie jego przekątne; konstrukcja zgodna z logiką pytania to narysowanie dwóch odcinków prostopadłych i połączenie ich końców. Zauważmy wreszcie, że bez zrozumienia sensu wynikania nie można zrozumieć skutku odwracania twierdzenia - operacji formalnej wykonywanej na zdaniu.
Kolejny etap budowania rozumienia dedukcji to odróżnianie argumentu ogólnego i argumentu w postaci szczególnych przypadków (przykładów). "Przekonaj mnie, że przekątne równoległoboku dzielą się na połowy." "Bo tak jest na przykład w prostokącie" - to często spotykana odpowiedź. To także argument nie do pogardzenia i często operujemy nim w życiu potocznym. Jednak argument "Bo gdyby wyciąć i obrócić cały równoległobok o 180o wokół punktu przecięcia przekątnych, wszystko nałoży się na siebie" ma zupełnie charakter: odnosi się do równoległoboku w ogóle, a nie do żadnego jego szczególnego przypadku. Podkreślę: chodzi o odróżnianie przez ucznia tych dwu typów argumentacji, a potem docenianie zalet argumentu ogólnego, nie zaś o wyeliminowanie podpierania się przykładem, gdy braknie czegoś lepszego. Tym bardziej, że przykład przykładowi nierówny, a ogólność można stopniować.
Po argument ogólny uczeń powinien nauczyć się sięgać przede wszystkim do definicji. Dotychczas omówione etapy są w istocie uniwersalne: dotyczą dedukcji w ogóle, nie tylko w matematyce. Ten jest specyficzny dla matematyki, wiąże się bowiem ze szczególną rolą definicji matematycznej. Rzadko służy ona wyjaśnieniu, czym jest badane pojęcie; brak definicji nie przeszkadza też w operowaniu pojęciem. Natomiast bez definicji nie jest możliwa dedukcja. Wielokąt wypukły jest pojęciem dającym się łatwo uchwycić na podstawie rysunkowych przykładów. Wtedy też można o wielokącie wypukłym z poczuciem pewności wypowiedzieć np. to, że wszystkie jego kąty są wypukłe. Operując przykładami można nabyć pewności, że część wspólna dwóch wielokątów wypukłych jest zawsze wielokątem wypukłym. Jednak argument ogólny, tj. dowód, musi oprzeć się na definicji. Oczywiście, w wielu przypadkach definicja nie wystarcza jako podstawa dedukcji, a w innych skuteczniejszego argumentu dostarcza wcześniej poznane twierdzenie. Jednak z reguły w łatwych przypadkach definicja jest najlepszym, jeżeli nie jedynym "ratunkiem".
Sądzę, że osiągnięcie przez większość uczniów tego etapu rozumienia matematycznej dedukcji w obecnych warunkach szkoły ogólnokształcącej jest możliwe, wymaga jednak systematycznej, wieloletniej pracy nauczycieli wszystkich trzech etapów kształcenia. Usiłowania prowadzące do zrozumienia, czym naprawdę jest dowód, mogą przynieść korzyść - jak myślę - tylko nielicznym, toteż podejmować je warto tylko w grupach uczniów o ponadprzeciętnych zainteresowaniach matematycznych. Proponuję świadomą rezygnację z "nauki dowodzenia" i skupienie się w nauczaniu na
Śledzenie, uczenie się i tworzenie dowodów zastąpmy tłumaczeniem dostrzeżonej własności i stopniowym ulepszaniem tłumaczenia. Taki kierunek umożliwia stały aktywny udział wszystkich uczniów: każdy może próbować lepiej wyjaśnić, każdy może wskazywać dostrzeżone wady w wyjaśnieniu kolegi czy nauczyciela a różne wyjaśnienia porównywać i wartościować. Na tej drodze rola definicji i twierdzeń w argumentacji powinna sama wypłynąć.
Zobaczmy to na przykładzie twierdzenia Pitagorasa. Żaden ze znanych jego dowodów nie mieści się w programie nauczania gimnazjum. Nauczyciel poprzestaje więc na pokazaniu uczniom, jak z rozciętych odpowiednio dwu kartonowych kwadratów ułożyć jeden większy. To tłumaczenie zadowala większość lub wszystkich uczniów. Można zburzyć ich pewność, pokazując znany paradoks: "trójkąt" o podstawie 10 i wysokości 13, ułożony z czterech części kwadratu o boku 8 zdaje się mieć pole o jednostkę większe od pola tego kwadratu. Zrozumieją, że trzeba wytłumaczyć, dlaczego części naprawdę przylegają do siebie i tworzą kwadrat. Ogólny przypadek jest trudny, za to łatwo to zrobić dla trójkąta równoramiennego. A choć nie jest to dowód ogólny, będzie stanowiło wyższy poziom argumentacji od "układanki", lepsze wytłumaczenie twierdzenia.
Rozumowanie przez analogię jest postępowaniem o wiele bardziej uniwersalnym od dedukcji. W istocie nasze rozumienie świata to upodobnianie jednych zjawisk do innych; to tworzenie "namacalnych" modeli dla zjawisk, których nie pojmujemy. Tworzenie modeli to też podstawowa metoda każdej nauki. Czyż szkoła nie powinna rozwijać tego sposobu myślenia? Rozumowanie przez analogię jest ryzykowne. Nieostrożnie stosowane może prowadzić do fałszu i wszystkich jego konsekwencji. Czyż szkoła nie powinna uczyć ostrożności w korzystaniu z analogii?
Matematyka szczególnie dobrze nadaje się do nauki myślenia przez analogię, i to z kilku powodów.
Przykład 1. Mnożenie jest pod wieloma względami analogiczne do dodawania, a związki mnożenia z dodawaniem analogiczne do związków potęgowania z mnożeniem. A więc np.
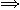 a =
(1/n)b to tak, jak
an = b
a =
(1/n)b to tak, jak
an = b 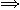 a =
b1/n
a =
b1/nCzy nie warto, by uczniowie te analogie dostrzegli, a ostatni wzór (na iloczyn wyrazów postępu geometrycznego) przez analogię utworzyli? A równocześnie uświadomili sobie, że związek potęgowania z dodawaniem nie jest analogiczny do związku mnożenia z dodawaniem, a więc
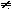 an
+ bn, chociaż
a(b + c) = ab + ac.
an
+ bn, chociaż
a(b + c) = ab + ac.
Przykład 2. Wzory na objętość równoległościanu i ostrosłupa są analogiczne do wzorów na pole równoległoboku i trójkąta. (Można je też analogicznie wyprowadzić, ale to osobna analogia.) Czy wzór na objętość ostrosłupa ściętego lub stożka ściętego, utworzony analogicznie do wzoru na pole trapezu, jest poprawny? Czy objętość ta jest więc równa iloczynowi średniej pól podstaw przez wysokość?
Przykład 3. Jaka linia na walcu lub sferze ma własności najbardziej przypominające prostą na płaszczyźnie?
Przykład 4. Jakie przekształcenia przestrzeni można uważać za analogiczne do symetrii środkowej (symetrii osiowej, obrotu) płaszczyzny?