- Pokazanie co, jak i dlaczego matematyzuje się na gruncie w rachunku
prawdopodobieństwa. Ukazanie osobliwych obiektów i środków matematyzacji,
a także motywacji dla konstrukcji przestrzeni probabilistycznych jako
modeli pewnych realnych sytuacji i towarzyszących im stosunków ilościowych
i jakościowych. Ukazanie pojęć i metod stochastycznych (w tym także
wnioskowań statystycznych) jako specyficznych matematycznych narzędzi
opisu i badania rzeczywistości. Uznanie tego celu za podstawowy wynika z
faktu, że kurs adresowany jest do studentów przygotowujących się do zawodu
nauczyciela matematyki.
- Prezentacja rachunku prawdopodobieństwa jako teorii dedukcyjnej
(ukazywanie nie tyle gotowej teorii aksjomatycznej ile procesu aksjomatyzacji).
- Kształtowanie intuicji stochastycznych, jako ważnego dziś aspektu
matematycznej kultury, poprzez odpowiednią organizację procesu wnioskowania
(zarówno w probabilistyce, jak i w statystyce matematycznej) w trakcie
rozwiązywania zadań powstałych na tle specyficznych sytuacji problemowych.
- Przygotowanie studentów do nauczania rachunku prawdopodobieństwa
wraz z elementami statystyki matematycznej poprzez prezentację stochastyki
nie jako gotowej teorii, ale poprzez jej tworzenie w trakcie rozwiązywania
problemów.
- Ukazanie autentycznego procesu stosowania matematyki (procesy
decyzyjne w sytuacjach ryzyka i ich stochastyczne modele, weryfikacja
hipotez, prawdopodobieństwo jako ocena ryzyka i decyzje wynikające z jego
wielkości, oceny oczekiwanych zysków i strat w grach hazardowych,
estymacja i jej wiarygodność, metody Monte Carlo).
Materiał obejmuje treści zaliczane do stochastyki rozumianej jako
fuzja elementów rachunku prawdopodobieństwa i statystyki matematycznej, a
także -- w pewnym zakresie -- elementów kombinatoryki i statystyki opisowej.
| SEMESTR 6 | TREŚCI NAUCZANIA |
- Przestrzeń probabilistyczna ziarnista (dyskretna) jako para
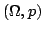 , gdzie
, gdzie 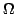 -- zbiór co najmniej dwuelementowy i co najwyżej
przeliczalny, a
-- zbiór co najmniej dwuelementowy i co najwyżej
przeliczalny, a 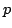 -- funkcja ze zbioru
-- funkcja ze zbioru 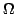 w zbiór liczb
rzeczywistych, nieujemna i taka, że
w zbiór liczb
rzeczywistych, nieujemna i taka, że
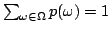 .
Doświadczenie losowe jako obiekt realnego świata. Przestrzeń
probabilistyczna jako model doświadczenia losowego. Drzewo stochastyczne jako
środek konstrukcji przestrzeni probabilistycznej. Drzewo a podstawowe
pojęcia i wzory kombinatoryczne. Graf stochastyczny jako środek konstrukcji
przestrzeni probabilistycznej (graf jako środek matematyzacji).
Produkt kartezjański przestrzeni probabilistycznych.
Klasyczne rozkłady prawdopodobieństwa na zbiorach skończonych.
Tablice liczb losowych. Losowanie próbki. Różne przyrządy
losujące jako generatory rozkładów prawdopodobieństwa. Izomorfizm
przestrzeni probabilistycznych. Symulacja stochastyczna oparta na
tablicach liczb losowych. Gra losowa typu totolotka a stochastyczny
model procesu podejmowania decyzji w sytuacjach ryzyka.
.
Doświadczenie losowe jako obiekt realnego świata. Przestrzeń
probabilistyczna jako model doświadczenia losowego. Drzewo stochastyczne jako
środek konstrukcji przestrzeni probabilistycznej. Drzewo a podstawowe
pojęcia i wzory kombinatoryczne. Graf stochastyczny jako środek konstrukcji
przestrzeni probabilistycznej (graf jako środek matematyzacji).
Produkt kartezjański przestrzeni probabilistycznych.
Klasyczne rozkłady prawdopodobieństwa na zbiorach skończonych.
Tablice liczb losowych. Losowanie próbki. Różne przyrządy
losujące jako generatory rozkładów prawdopodobieństwa. Izomorfizm
przestrzeni probabilistycznych. Symulacja stochastyczna oparta na
tablicach liczb losowych. Gra losowa typu totolotka a stochastyczny
model procesu podejmowania decyzji w sytuacjach ryzyka.
- Zdarzenie jako pojęcie matematyczne. Algebra zdarzeń. Układ zupełny
zdarzeń. Definicja prawdopodobieństwa zdarzenia w ziarnistej
przestrzeni probabilistycznej
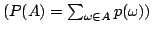 .
Własności prawdopodobieństwa. Zdarzenia praktycznie
niemożliwe. Zdarzenia praktycznie pewne. Prawdopodobieństwo zdarzenia jako
matematyczne narzędzie rozwiązywania konkretnych problemów.
Prawdopodobieństwo jako ocena pewnego ryzyka. Prawdopodobieństwo jako
narzędzie weryfikacji hipotez. Różne aspekty
prawdopodobieństwa (klasyczny,
miarowy, statystyczny, idea stochastycznego grafu przepływu).
Prawdopodobieństwo klasyczne. Gra strategiczno-losowa jako model
procesu decyzyjnego. Prawdopodobieństwo a sprawiedliwość gry losowej.
Prawdopodobieństwo geometryczne. Aksjomatyzacja rachunku prawdopodobieństwa.
Aksjomatyczna definicja przestrzeni probabilistycznej.
.
Własności prawdopodobieństwa. Zdarzenia praktycznie
niemożliwe. Zdarzenia praktycznie pewne. Prawdopodobieństwo zdarzenia jako
matematyczne narzędzie rozwiązywania konkretnych problemów.
Prawdopodobieństwo jako ocena pewnego ryzyka. Prawdopodobieństwo jako
narzędzie weryfikacji hipotez. Różne aspekty
prawdopodobieństwa (klasyczny,
miarowy, statystyczny, idea stochastycznego grafu przepływu).
Prawdopodobieństwo klasyczne. Gra strategiczno-losowa jako model
procesu decyzyjnego. Prawdopodobieństwo a sprawiedliwość gry losowej.
Prawdopodobieństwo geometryczne. Aksjomatyzacja rachunku prawdopodobieństwa.
Aksjomatyczna definicja przestrzeni probabilistycznej.
- Typowe schematy losowe i przestrzenie probabilistyczne jako ich modele.
Próba Bernoullie'ego. Schemat Bernoullie'ego. Oczekiwanie na pierwszy sukces.
Schemat kolekcjonera. Schemat Ehrenfestów. Schematy urnowe a losowe
rozmieszczenia. Graf stochastyczny danego schematu losowego.
- Prawdopodobieństwo warunkowe. Prawdopodobieństwo całkowite.
Prawdopodobieństwo warunkowe a posteriori. Relacje ,,zwiększa
szanse'', ,,zmiejsza szanse'' i ich paradoksalne własności. Zdarzenia
stochastycznie niezależne. Niezależność stochastyczna parami.
Niezależność zespołowa.
- Zmienna losowa w ziarnistej przestrzeni probabilistycznej.
Wygrana w grze jako zmienna losowa. Czas trwania doświadczenia losowego
o losowej liczbie etapów jako zmienna losowa. Rozkład zmiennej losowej.
Przestrzeń probabilistyczna generowana na prostej przez zmienną
losową ziarnistą. Rozkład dwumianowy. Rozkład czasu oczekiwania na
pierwszy sukces jako rozkład geometryczny.
Wartość oczekiwana zmiennej losowej,
czyli nadzieja matematyczna. Wartość oczekiwana a gry sprawiedliwe oraz
prosperowanie gier hazardowych. Wariancja. Odchylenie standardowe. Moda.
Gra jako model procesu podejmowania decyzji w sytuacjach ryzyka.
Maksymalizacja średnich korzyści jako kryterium ustalania decyzji optymalnej.
- Prawo wielkich liczb Bernoulliego. Prawo wielkich liczb a
szacowanie prawdopodobieństwa zdarzenia za pomocą jego częstości.
- Populacja generalna. Cecha. Rozkład cechy w populacji. Wartość średnia
cechy. Próbka czyli dane statystyczne. Gromadzenie i opracowywanie próbki.
Elementy statystyki opisowej. Próbka losowa. Estymator. Średnia z próbki jako
estymator.
Metoda największej wiarygodności na przykładzie szacowania nieznanej liczby
czarnych kul w urnie (liczby wadliwych sztuk w partii towaru).
Proste przykłady weryfikacji hipotez. Konstrukcja regulaminu wiarygodnego
oceniania rezultatów testowych sprawdzianów wiedzy.
Rozstrzyganie środkami matematycznymi czy dany fakt jest rezultatem wiedzy, talentu,
czy też przypadku (np. zgadywania).
- Gra losowa jako środek matematycznej aktywizacji ucznia.
Stochastyczne zadania jako ilustracja autentycznego procesu stosowania
matematyki. Rysunek jako narzędzie matematyzacji i argumentacji w rachunku
prawdopodobieństwa. Dane statystyczne jako inspiracja matematycznej
działalności (refleksja a posteriori, wyjaśnianie na gruncie
rachunku prawdopodobieństwa pewnych zaskakujących faktów ujawnionych przez
dane statystyczne). Zadania stochastyczne -- niespodzianki a kształtowanie
pojęć i intuicji stochastycznych. Przyrządy losujące jako generatory rozkładów
prawdopodobieństwa i jako nośniki ogólnomatematycznych struktur. Nieprzechodnie
kostki B. Efrona. Gry Penney'a i paradoksy z nimi związane. Informacje o
niektórych koncepcjach nauczania rachunku prawdopodobieństwa (A. Engla,
H. Freudenthala,
L. Röade,
T. Varga).
- D. Bobrowski, Probabilistyka w zastosowaniach
technicznych, WN-T, Warszawa 1986.
- W. Feller, Wstęp do rachunku prawdopodobieństwa, t. I, PWN,
Warszawa 1987.
- M. Fisz, Rachunek prawdopodobieństwa i statystyka
matematyczna, PWN, Warszawa 1958.
- H. Kąkol, Podstawowe pojęcia statystyki i rachunku
prawdopodobieństwa. Propozycja dydaktyczna, WN WSP, Kraków 1990.
- H. Kąkol, Elementy statystyki opisowej w szkole
podstawowej, Wyd. Dla Szkoły, Bielsko-Biała 1994.
- L. T. Kubik, Rachunek prawdopodobieństwa. Podręcznik dla
kierunków nauczycielskich studiów matemtycznych, PWN, Warszawa 1986.
- E. Łakoma, Historyczny rozwój pojęcia
prawdopodobieństwa, CODN, Warszawa 1992.
- A. Płocki, Prawdopodobieństwo wokół nas, Wyd. Dla Szkoły,
Bielsko-Biała, 1977.
- A. Płocki, Propedeutyka rachunku prawdopodobieństwa i
statystyki matematycznej dla nauczycieli, PWN, Warszawa 1992.
- A. Płocki, Stochastyka 1. Rachunek prawdopodobieństwa i
statystyka matematyczna jako matematyka ,,in statu nascendi'', WN WSP,
Kraków 1997.
- A. Żak, T. Zakrzewski, Kombinatoryka, prawdopodobieństwo i
zdrowy rozsądek, Quadrivium, Wrocław 1994.
| SEMESTR 7 | TREŚCI NAUCZANIA |
- Aksjomatyczne ujęcie rachunku prawdopodobieństwa. Przestrzeń
probabilistyczna jako system miary unormowanej. Prawdopodobieństwo jako
miara unormowana. Zmienna losowa w dowolnej przestrzeni probabilistycznej
jako funkcja mierzalna. Rozkład zmiennej losowej jako miara unormowana
generowana na prostej przez funkcję mierzalną. Dystrybuanta zmiennej losowej.
Zmienna losowa ciągła. Momenty zmiennej losowej ciągłej.
- Twierdzenie Poissona. Rozkład Poissona. Przybliżenie Poissona.
Rozkład prostokątny. Rozkład normalny Gaussa. Rozkład wykładniczy.
Zbieżność stochastyczna. Prawo wielkich liczb Bernoullego. Prawo wielkich
liczb Chinczyna. Twierdzenie de Moivre'a-Laplace'a.
- Zmienna losowa wielowymiarowa, czyli wektor losowy. Rozkład
wektora losowego. Rozkłady brzegowe. Rozkłady warunkowe. Zmienne losowe
niezależne. Funkcja charakterystyczna zmiennej losowej. Funkcja
charakterystyczna a momenty. Funkcja charakterystyczna a rozkład sumy
niezależnych zmiennych losowych.
- Stochastyczny model procesu podejmowania decyzji w warunkach
ryzyka. Macierz korzyści. Gra strategiczno-losowa jako model procesu decyzyjnego.
- Symulacje oparte na tablicach liczb losowych. Metody Monte Carlo.
- Łańcuch Markowa jako szczególny schemat losowy. Graf stochastyczny
jako środek opisu i badania łańcucha Markowa. Wektor początkowy i
macierz prawdopodobieństw przejść. Rachunek algebraiczny a rozkład stanów
w chwili
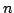 . Grafy Engla. Rozwijanie grafu stochastycznego w czasie.
Dwuwymiarowy graf stochastyczny. Rozkład stanów w chwili
. Grafy Engla. Rozwijanie grafu stochastycznego w czasie.
Dwuwymiarowy graf stochastyczny. Rozkład stanów w chwili 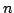 . Jednorodny
łańcuch Markowa. Stacjonarny łańcuch Markowa. Redukcje grafu stochastycznego.
Algorytm pochłaniania dla grafu stochastycznego o niepustym brzegu. Czas
błądzenia po grafie stochastycznym jako zmienna losowa. Algorytm średniego
czasu błądzenia po grafie. Czekanie na serie sukcesów i porażek jako
łańcuch Markowa. Gry Penney'a.
. Jednorodny
łańcuch Markowa. Stacjonarny łańcuch Markowa. Redukcje grafu stochastycznego.
Algorytm pochłaniania dla grafu stochastycznego o niepustym brzegu. Czas
błądzenia po grafie stochastycznym jako zmienna losowa. Algorytm średniego
czasu błądzenia po grafie. Czekanie na serie sukcesów i porażek jako
łańcuch Markowa. Gry Penney'a.
- Populacja. Cecha. Próbka. Statystyka. Konstrukcja rozkładu
statystyki za pomocą funkcji charakterystycznej. Estymator.
Estymacja. Estymator zgodny. Estymator nieobciążony. Statystyka
średnia z próbki. Rozkład statystyki średnia z próbki w przypadku cechy o
rozkładzie normalnym a funkcja charakterystyczna. Wariancja z próbki. Metoda
momentów. Metoda największej wiarygodności. Poziom ufności. Metoda przedziałów
ufności. Poziom istotności. Test istotności. Obszar krytyczny. Pearsona test
zgodności. Test niezależności.
- Kształtowanie pojęć stochastycznych jako problem dydaktyki
matematyki.
Wnioskowania przez symetrie i analogie w stochastyce.
Pojęcia i metody stochastyczne w nauczaniu matematyki a ilustracja
procesu stosowania matematyki. Stochastyczne paradoksy i sofizmaty.
Zadania stochastyczne jako nowy element kształcenia matematycznego. Znane z
historii i współczesności gry losowe jako źródło idei i zadań stochastycznych.
Przyrządy losujące jako generatory rozkładów prawdopodobieństwa.
Kostka i moneta jako generatory klasycznych rozkładów prawdopodobieństwa
na dowolnych skończonych zbiorach -- losowanie próbki.
- D. Bobrowski, Probabilistyka w zastosowaniach
technicznych, WN-T, Warszawa 1986.
- W. Feller, Wstęp do rachunku prawdopodobieństwa, t. I, PWN,
Warszawa 1987.
- M. Fisz, Rachunek prawdopodobieństwa i statystyka
matematyczna, PWN, Warszawa 1958.
- M. Iosifescu, Skończone procesy Markowa i ich
zastosowanie, PWN, Warszawa 1988.
- L. T. Kubik, Rachunek prawdopodobieństwa. Podręcznik dla
kierunków nauczycielskich studiów matematycznych, PWN, Warszawa 1986.
- J. Ombach, Wstęp do rachunku
prawdopodobieństwa, Wydawnictwo IM AGH, 1997.
- A. Płocki, Prawdopodobieństwo wokół nas. Rachunek
prawdopodobieństwa w zadaniach i problemach, Wyd. ,,Dla Szkoły'', Bielsko-Biała
1997.
- A. Płocki, Propedeutyka rachunku prawdopodobieństwa i
statystyki matematycznej dla nauczycieli, PWN, Warszawa 1992.
- A. Płocki, Stochastyka 1. Rachunek prawdopodobieństwa i
statystyka matematyczna jako matematyka in statu nascendi, WN WSP, Kraków 1997.
- A. Płocki, Stochastyka 2. Rachunek prawdopodobieństwa i
statystyka matematyczna -- Zarys dydaktyki, WN WSP, Kraków 1997.
- J. Stojanov (i in.), Zbiór zadań z rachunku prawdopodobieństwa, PWN, Warszawa 1992.
Instytut Matematyki Akademii
Pedagogicznej w Krakowie,
15.01.2002








