Nadrzędny dokument:	PRACA MAGISTERSKA ORAZ EGZAMIN MAGISTERSKI
Poprzedni dokument:	Zalecenia do pisania, prowadzenia i oceny prac magisterskich oraz licencjackich z matematyki i dydaktyki matematyki

Wymagania do egzaminu magisterskiego

WYMAGANIA OBOWIĄZUJĄ OD ROKU AKADEMICKIEGO 2003/4

Na egzaminie magisterskim student powinien wykazać się znajomością i dobrym rozumieniem podstawowych pojęć matematycznych i ich własności oraz znajomością podstawowych zagadnień z dydaktyki matematyki. Ponadto powinien dobrze operować językiem matematycznym, umieć przedstawić syntetycznie kluczowe problemy matematyki wyższej, a także widzieć związki matematyki wyższej z matematyką elementarną.

Każdy student powinien być przygotowany do odpowiedzi na wszystkie zagadnienia działu I oraz wszystkie zagadnienia z wybranego przez siebie i uzgodnionego z promotorem jednego z działów: II, III, IV, V i VI (studenci o specjalności Matematyka z Informatyką -- również z działu VII). Wybór tego działu musi być zgłoszony przy składaniu pracy (w szczególności po to, aby w egzaminie mógł uczestniczyć specjalista z informatyki, jeżeli student wybrał dział VII). Na wniosek studenta i promotora Dyrektor Instytutu może wyznaczyć studentowi indywidualne pensum do egzaminu magisterskiego, które zastąpi wybór jednego z działów II-VII (dział I pozostaje obowiązkowy).

I. Pojęcia i wiadomości podstawowe

1. Pojęcia teorii aksjomatycznej i jej modelu.
2. Elementarne pojęcia rachunku zdań.
3. Aksjomatyczny system teorii mnogości.
4. Liczby kardynalne i porządkowe.
5. Relacje równoważnościowe i porządkowe. Definiowanie pojęć matematycznych za pomocą relacji równoważnościowych. Uporządkowanie podstawowych zbiorów liczbowych.
6. Systemy aksjomatyczne arytmetyki liczb naturalnych. Konstrukcja zbioru liczb naturalnych w teorii mnogości. Konstrukcje podstawowych struktur liczbowych (liczby całkowite, wymierne, rzeczywiste i zespolone).
7. Aksjomatyczne ujęcie geometrii elementarnej. Różne geometrie i ich modele.
8. Geometria krzywych. Krzywe regularne, długość krzywej, trójścian Freneta.
9. Geometria powierzchni. Wektor normalny, płaszczyzna styczna, pole płata.
10. Definicje i modele podstawowych struktur algebraicznych, struktury ilorazowe.
11. Homomorfizmy struktur algebraicznych. Podstawowe własności oraz przykłady w poszczególnych strukturach.
12. Przestrzeń wektorowa, jej baza i wymiar; podprzestrzeń generowana przez zbiór; przykłady.
13. Algebra macierzy, wyznaczniki i układy równań liniowych.
14. Układy współrzędnych w przestrzeniach afinicznych i euklidesowych. Równania prostych i płaszczyzn.
15. Przekształcenia afiniczne.
16. Krzywe i powierzchnie stopnia 2.
17. Aksjomatyka rachunku prawdopodobieństwa. Prawdopodobieństwo warunkowe, prawdopodobieństwo całkowite, wzór Bayesa. Niezależność zdarzeń. Przykłady przestrzeni probabilistycznych.
18. Zmienne losowe jedno- i dwuwymiarowe i generowane przez nie przestrzenie probabilistyczne na prostej i na płaszczyźnie. Niezaleźność zmiennych losowych. Dystrybuanta. Wartość oczekiwana i wariancja.
19. Różne rodzaje zbieżności. Prawo wielkich liczb Bernoulliego. Twierdzenia graniczne.
20. Różne definicje granicy ciągu i granicy funkcji. Podstawowe własności granic ciągów funkcji.
21. Szeregi liczbowe. Kryteria zbieżności.
22. Różne definicje ciągłości funkcji. Własności funkcji ciągłych.
23. Topologia i sposoby jej wprowadzania. Odwzorowania ciągłe i homeomorfizmy.
24. Pochodna funkcji jednej zmiennej. Ekstrema funkcji, wypukłość. Twierdzenia o wartości średniej i ich zastosowania. Wzór Taylora.
25. Różniczki funkcji wielu zmiennych, pochodne cząstkowe, pochodna kierunkowa.
26. Funkcje analityczne, twierdzenie całkowe Cauchy'ego, wzór całkowy Cauchy'ego, ich konsekwencje.
27. Proces całkowy w definicjach różnego rodzaju całek (wielokrotnych, krzywoliniowych, powierzchniowych).
28. Przestrzenie Banacha. Podstawowe przykłady przestrzeni ciągowych i funkcyjnych oraz operatorów liniowych ciągłych na tych przestrzeniach.
29. Miara i jej podstawowe własności. Miara Lebesgue'a, miara Jordana.

30. Poziomy i kryteria rozumienia pojęć. Typy rozumowań w nauczaniu matematyki (wnioskowanie empiryczne, intuicyjne i formalne, indukcja, dedukcja, redukcja, rozumowanie nie wprost).
31. Rodzaje zadań matematycznych w różnych koncepcjach nauczania, główne etapy wg. Polyi i przykłady wskazówek heurystycznych w procesie rozwiązywania zadań.
32. Cele nauczania matematyki, rola pojęciowego i algorytmicznego ujęcia matematyki w różnych koncepcjach nauczania.
33. Dydaktyczne problemy związane z definiowaniem i korzystaniem z definicji, formułowaniem twierdzeń, ich stosowaniem i dowodzeniem.
34. Wykorzystanie technologii informacyjnej w nauczaniu matematyki, przykłady edukacyjnych programów komputerowych.

II. Analiza matematyczna i topologia

1. Różne rodzaje przestrzeni topologicznych (przestrzenie zwarte, spójne, zupełne, ośrodkowe); aksjomaty oddzielania.
2. Własności funkcji ciągłych rzeczywistych, określonych na przestrzeniach metrycznych.
3. Własności granic ciągów funkcyjnych i sum szeregów funkcyjnych.
4. Ekstrema i ekstrema warunkowe dla funkcji wielu zmiennych.
5. Zastosowanie twierdzenia Liouville'a do dowodu zasadniczego twierdzenia algebry.
6. Twierdzenie o identyczności funkcji analitycznych. Twierdzenie o zachowaniu obszaru dla funkcji analitycznych. Zastosowana tych twierdzeń.
7. Miara zewnętrzna, twierdzenie Caratheodory'ego, miara Lebesgue'a i jej własności.
8. Całka Lebesgue'a, własności i związek z całką Riemanna.
9. Twierdzenia o istnieniu i jednoznaczności rozwiązań równań różniczkowych.
10. Przykłady metod rozwiązywania pewnych typów równań różniczkowych pierwszego i drugiego rzędu.
11. Przestrzenie Banacha i Hilberta jako przykłady łączenia struktury topologicznej i liniowej. Operatory i funkcjonały liniowe ciągłe.
12. Szeregi Fouriera w przestrzeni Hilberta. Kryteria zbieżności dla funkcji rzeczywistych.

III. Algebra

1. Grupy i pierścienie, dzielniki normalne i ideały, struktury ilorazowe.
2. Element pierwszy i nierozkładalny; pierścień Gaussa, pierścień główny, pierścień noetherowski, pierścień Dedekinda.
3. Przywiedlność i nieprzywiedlność wielomianów nad danymi pierścieniami.
4. NWP i NWW. Pierścienie Euklidesa i algorytm Euklidesa.
5. Elementy algebraiczne i elementy przestępne nad ciałem; rozszerzenia algebraiczne, rozszerzenia skończone, rozszerzenie o element algebraiczny.
6. Ciała algebraicznie domknięte. Zasadnicze twierdzenie algebry.
7. Przestrzenie euklidesowe; od iloczynu skalarnego przez normę do metryki; ortogonalność; postać iloczynu skalarnego.
8. Izometrie, własności, reprezentacje, macierze ortogonalne, przykłady.
9. Postacie kanoniczne formy kwadratowej. Własności. Formy kwadratowe dodatnio określone.
10. Macierz przekształcenia liniowego względem danych baz, rząd przekształcenia.

IV. Geometria

1. Pojęcie geometrii w sensie Kleina. Podstawowe niezmienniki grup przekształceń rzutowych, afinicznych i euklidesowych (izometrii).
2. Twierdzenie o rozkładzie izometrii na symetrie względem hiperpłaszczyzn.
3. Klasyfikacja izometrii przestrzeni $\mbox{$\mathbb{R}$}^2$ i $\mbox{$\mathbb{R}$}^3$.
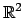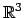4. Izometrie własne wielokątów i wielościanów foremnych.
5. Warunki wykonalności konstrukcji cyrklem i linijką.
6. Konstruowalność wielokątów foremnych. Złoty podział.
7. Warunki rownoważne V postulatowi Euklidesa.
8. Dualność w geometrii rzutowej. Przykłady twierdzeń dualnych.
9. Dwustosunek czwórki punktow. Czworokąt zupełny. Punkty harmoniczne.
10. Przykłady powierzchni orientowalnych i nieorientowalnych.
11. Powierzchnie o stałej krzywiźnie.
12. Formy fundamentalne.
13. Pojęcie geodezyjnych i przykłady.

V. Rachunek prawdopodobieństwa z elementami statystyki matematycznej

1. Przestrzeń probabilistyczna (definicja aksjomatyczna). Ziarnista (dyskretna) przestrzeń probabilistyczna. Przestrzeń probabilistyczna jako model doświadczenia losowego.
2. Zmienna losowa jedno- (dwu-) wymiarowa i generowana przez nią przestrzeń probabilistyczna na prostej (na płaszczyźnie).
3. Szeregi liczbowe i funkcyjne w rachunku prawdopodobieństwa. Funkcja charakterystyczna zmiennej losowej. Momenty zmiennej losowej.
4. Twierdzenia graniczne.
5. Podstawowe rozkłady prawdopodobieństwa i przykłady przestrzeni probabilistycznych o tych rozkładach (rozkład Bernoulliego, Poissona, normalny, itd.).
6. Populacja. Cecha. Próba. Statystyka. Estymacja i weryfikacja hipotez -- na przykładach adresowanych do szkoły.

VI. Dydaktyka matematyki

1. Reprezentacje enaktywne, ikoniczne i symboliczne i ich rola w prosesie kształtowania pojęć matematycznych.
2. Specyfika języka szkolnej matematyki, charakterystyczne błędy popełniane przez uczniów i sposoby ich wykorzystywania w procesie kształtowania pojęć.
3. Lokalna dedukcja na lekcjach matematyki.
4. Środki poglądowe specyficzne dla matematyki szkolnej.
5. Czynnościowe nauczanie matematyki.
6. Elementy logiki w nauczaniu matematyki.
7. Metodyka nauki o liczbie i działaniach.
8. Metodyka nauki o funkcjach numerycznych i ich wykresach.
9. Metodyka nauki o przekształceniach geometrycznych.
10. Równania i nierówności w matematyce elementarnej.

VII. Informatyka

1. Najpopularniejsze systemy operacyjne - przeznaczenie, krótka charakterystyka.
2. Typowe struktury danych używane w językach programowania.
3. Procedura jako element strukturalizacji algorytmu.
4. Iteracja a rekurencja.
5. Metody translacji programów komputerowych - kompilacja, interpretacja - podstawowe różnice.
6. Definicja algorytmu, cechy poprawnych algorytmów, przykłady.
7. Podobieństwa i różnice programów użytkowych.
8. Program użytkowy jako narzędzie pracy biurowej - przykłady zastosowań.
9. Program użytkowy w edukacji - przykłady zastosowań.
10. Alternatywa dla Microsoft Office - przykłady innych pakietów biurowych, w tym dostępnych bezpłatnie (freeware).
11. Wybrane problemy ochrony danych - wirusy i ochrona przed ich atakami.
12. Internet jako narzędzie komunikacji i źródło wiedzy - typowe usługi.
13. Elementy budowy komputera - przykłady urządzeń wewnętrznych i zewnętrznych.
14. Przechowywanie informacji - jednostki pamięci, rodzaje pamięci, przykładowe nośniki.
15. Legalność oprogramowania - aspekty prawne i etyczne.
16. Przykładowy program przedmiotu ,,Elementy informatyki'' dla wybranej klasy.
17. Propozycja przebiegu lekcji informatyki z zakresu gimnazjum lub szkoły średniej.
18. Propozycja lekcji matematyki z wykorzystaniem komputera.
19. Przykładowe programy komputerowe do zastoswań podczas lekcji matematyki.
20. Przykłady zasobów internetowych dla nauczyciela matematyki.

Nadrzędny dokument:	PRACA MAGISTERSKA ORAZ EGZAMIN MAGISTERSKI
Poprzedni dokument:	Zalecenia do pisania, prowadzenia i oceny prac magisterskich oraz licencjackich z matematyki i dydaktyki matematyki