Wybrane zagadnienia z geometrii różniczkowej

TREŚCI NAUCZANIA

Celem seminarium jest nauka samodzielnej pracy z tekstem matematycznym oraz poznanie dalszych pojęć, przykładów, twierdzeń i metod, nie omawianych na wykładzie specjalnym. Realizacji tego celu ma służyć przede wszystkim samodzielne opracowanie i prezentacja jakiegoś tematu - na przykład z poniższej listy, a także wysłuchanie referatów przygotowanych przez innych uczestników seminarium.

1. Twierdzenie Frobeniusa (różne ujęcia - w języku pól wektorowych, w języku form różniczkowych).
2. Twierdzenie Gaussa-Bonneta.
3. Rozmaitości zespolone. Rozmaitości hermitowskie i kählerowskie.
4. Grupy Liego i algebry Liego.
5. Powierzchnie o stałej krzywiźnie. Przekształcenie Bäcklunda.
6. Powierzchnie minimalne.
7. Krzywe i powierzchnie wypukłe. Przykład związku wielkości zdefiniowanych lokalnie z globalnymi własnościami rozmaitości.
8. Immersje afiniczne, metryka Blaschke, afiniczne pole normalne.

LITERATURA PODSTAWOWA

1. M. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall Inc., Englewood Cliffs, New Jersey 1976.
2. J. Gancarzewicz, Geometria różniczkowa, PWN, Warszawa 1987.
3. J. Gancarzewicz i B. Opozda, Wstęp do geometrii różniczkowej, Wydawnictwo UJ, Kraków 2003.
4. A. Goetz, Geometria różniczkowa, PWN, Warszawa 1972.
5. S. Kobayashi, K. Nomizu, Foundations of Differential Geometry, vol. I, II, Interscience Publishers, New York - London 1963, 1969.
6. K. Nomizu, T. Sasaki, Affine differential geometry, Cambridge University Press 1994.
7. J. Oprea, Geometria różniczkowa i jej zastosowania, Wydawnictwo Naukowe PWN, Warszawa 2002.
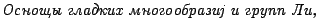
8. F. Warner, Foundations of Differentiable Manifolds and Lie Groups, Springer-Verlag, New York Berlin Heidelberg Tokyo 1983; przekład rosyjski: 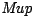Moskwa 1987.
9. S. S. Chern, W. H. Chén, Wēifēn jihé jiăngyì, Běijīng Dàxué Chūbănshè, Běijīng 2001.

LITERATURA UZUPEŁNIAJĄCA

Zależna od tematyki referatu i pracy magisterskiej.