Celem kursu jest gruntowne przyswojenie przez studentów
elementarnych działów analizy matematycznej tzn. rachunku
różniczkowego i całkowego funkcji zmiennych rzeczywistych
(jednej i wielu zmiennych). Wybór materiału pozwala
uwypuklić związki z innymi działami matematyki jak: geometria,
topologia, algebra, rachunek prawdopodobieństwa.
| SEMESTR 1 | TREŚCI NAUCZANIA |
- Liczby rzeczywiste.
Aksjomatyka liczb rzeczywistych. Kresy zbiorów.
- Odwzorowania. Składanie, odwracanie, obrazy i przeciwobrazy zbiorów.
Podstawowe funkcje elementarne w dziedzinie rzeczywistej, ciągi i
podciągi.
- Teoria granic.
Granica ciągu liczbowego. Granica dolna i górna ciągu liczbowego i funkcji
rzeczywistej w punkcie.
Przestrzenie metryczne, otoczenia punktów, zbiory otwarte i domknięte, punkty
skupienia.
Zwartość, spójność i zupełność podzbiorów przestrzeni euklidesowej.
- Odwzorowania ciągłe i ich własności.
Podstawowe funkcje elementarne w dziedzinie rzeczywistej, ich ciągłość i
granice z nimi związane.
Własność Darboux, ciągłość jednostajna.
| SEMESTR 2 | TREŚCI NAUCZANIA |
- Rachunek różniczkowy funkcji zmiennej rzeczywistej.
Interpretacja fizyczna i geometryczna pochodnej. Działania na
funkcjach a pochodna. Twierdzenia o wartości średniej. Reguła
de l'Hospitala. Wzór Taylora i jego zastosowania (ekstrema
lokalne, wypukłość).
Asymptoty, badanie przebiegu zmienności funkcji.
- Szeregi liczbowe.
Kryteria zbieżności szeregów. Zbieżność bezwzględna i warunkowa. Mnożenie
szeregów.
- Rachunek całkowy funkcji zmiennej rzeczywistej. Całka nieoznaczona.
Całkowanie elementarne.
Całka oznaczona. Własności całki oznaczonej. Warunki konieczne i
wystarczające całkowalności.
Zastosowanie geometryczne i fizyczne całki.
Całki niewłaściwe. Kryterium całkowe zbieżności szeregu.
| SEMESTR 3 | TREŚCI NAUCZANIA |
- Ciągi i szeregi funkcyjne.
Zbieżność punktowa i jednostajna ciągów i szeregów funkcyjnych.
Kryteria zbieżności jednostajnej szeregów funkcyjnych.
Ciągłość i różniczkowanie granicy ciągu funkcyjnego i sumy szeregu
funkcyjnego.
- Szeregi potęgowe.
Szereg Taylora i pojęcie funkcji analitycznej zmiennej rzeczywistej.
Rozwijanie w szereg Taylora podstawowych funkcji elementarnych.
- Szeregi Fouriera.
Zbieżność punktowa i jednostajna szeregów Fouriera. Kryteria zbieżności.
Przykłady rozwinięć.
Twierdzenie Weierstrassa dla odcinka.
- Odwzorowania z
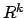 w
w 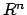 (granica, ciągłość).
(granica, ciągłość).
| SEMESTR 4 | TREŚCI NAUCZANIA |
- Rachunek różniczkowy (odwzorowania z
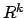 w
w 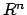 ).
Pochodne cząstkowe, kierunkowe i różniczkowalność funkcji.
Pochodna, jej sens geometryczny.
Macierz Jacobiego, jakobian i gradient.
Działania na odwzorowaniach a pochodne.
Pochodne wyższych rzędów. Twierdzenie o wartości średniej.
Wzór Taylora. Zastosowania do badania ekstremów lokalnych.
Twierdzenia o odwzorowaniu uwikłanym, o lokalnej odwracalności odwzorowania
klasy
).
Pochodne cząstkowe, kierunkowe i różniczkowalność funkcji.
Pochodna, jej sens geometryczny.
Macierz Jacobiego, jakobian i gradient.
Działania na odwzorowaniach a pochodne.
Pochodne wyższych rzędów. Twierdzenie o wartości średniej.
Wzór Taylora. Zastosowania do badania ekstremów lokalnych.
Twierdzenia o odwzorowaniu uwikłanym, o lokalnej odwracalności odwzorowania
klasy 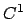 .
Ekstrema warunkowe lokalne.
.
Ekstrema warunkowe lokalne.
- Elementy geometrii różniczkowej.
Równania naturalne krzywych.
Prosta styczna i normalna do krzywej. Krzywizna.
| SEMESTR 5 | TREŚCI NAUCZANIA |
- Całki wielokrotne.
Całka Riemanna w
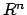 . Całki iterowane. Całki w obszarze normalnym i
regularnym.
Twierdzenie o zamianie zmiennych. Zastosowania geometryczne, obliczanie
objętości i pola płata
powierzchniowego. Zastosowania do fizyki.
. Całki iterowane. Całki w obszarze normalnym i
regularnym.
Twierdzenie o zamianie zmiennych. Zastosowania geometryczne, obliczanie
objętości i pola płata
powierzchniowego. Zastosowania do fizyki.
- Teoria miary.
Ciała, "sigma"-ciała, miara, zbiory borelowskie. Miara zewnętrzna.
Twierdzenie Caratheodory'ego.
Produktowanie miar.
Miara Lebesgue'a w
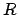 i w
i w 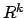 .
Własności miary Lebesgue'a. Funkcje mierzalne.
Informacje o mierze Jordana.
.
Własności miary Lebesgue'a. Funkcje mierzalne.
Informacje o mierze Jordana.
- Całka względem miary.
Warunek konieczny i dostateczny całkowalności w sensie Riemanna.
Twierdzenie Fubiniego i twierdzenie o podstawianiu. Twierdzenia o
przechodzeniu do granicy pod
znakiem całki. Całka Riemanna, a całka Lebesguea.
| SEMESTR 6 | TREŚCI NAUCZANIA |
- Całki krzywoliniowe i powierzchniowe. Całki krzywoliniowe pierwszego i
drugiego rodzaju. Warunki
niezależności całki od drogi całkowania. Wzór Greena. Orientacja powierzchni.
Całki powierzchniowe
pierwszego i drugiego rodzaju. Wzór Gaussa-Ostrogradzkiego. Elementy pola
wektorowego.
Formy różniczkowe i twierdzenie Stokesa.
- Pojęcie równania różniczkowego oraz jego rozwiązania, intrepretacja
geometryczna.Istnienie i
jednoznaczność rozwiązań równania różniczkowego. Przykłady równań
całkowalnych.Układy równań
różniczkowych liniowych.
| UWAGI O REALIZACJI PROGRAMU |
Wykład nie powinien
ograniczać się do podawania treści matematycznych wyłącznie w ich
abstrakcyjnej postaci, lecz jak najszerzej uwypuklać
źródła tych treści, w szczególności winien szeroko
nawiązywać do treści przyrodniczych, praktycznych oraz do matematyki
szkolnej.
Kolejność przerabianego materiału, jak i sposób jego ujęcia, pozostawia się
wykładającemu.
Musi on pamiętać o tym, że we właściwym czasie
powinien opracować wiadomości nieodzowne lub użyteczne dla innych
przedmiotów studiów (geometria, topologia, rachunek prawdopodobieństwa).
- J. Banaś, S. Wędrychowicz, Zbiór zadań z analizy
matematycznej, WN-T, Warszawa 1994.
- G. N. Berman, Zbiór zadań z analizy matematycznej, Wydawnictwo
Pracowni Komputerowej Jacka Skalmierskiego, Gliwice 1999.
- A. Birkholc, Analiza matematyczna, funkcje wielu zmiennych, PWN,
Warszawa 1986.
- B. P. Demidowicz, Sbornik zadacz i uprażnienij po matemematiczeskomu
analizu, Izdat. Nauka, Moskwa 1977.
- G. M. Fichtenholz, Rachunek różniczkowy i całkowy, t. I,II,III, PWN,
Warszawa 1985.
- W. Kołodziej, Analiza matematyczna, PWN, Warszawa 1978.
- T. Krasiński, Analiza matematyczna (funkcje jednej
zmiennej), WUŁ, Łódź 2003.
- W. Krysicki, L. Włodarski, Analiza matematyczna w zadaniach,
cz. I,II, PWN, Warszawa 1994.
- F. Leja, Rachunek różniczkowy i całkowy, PWN,
Warszawa 1976.
- W. Rudin, Podstawy analizy matematycznej, PWN,
Warszawa 1982.
- R. Sikorski, Rachunek różniczkowy i całkowy (funkcji wielu
zmiennych), PWN, Warszawa 1967.
- S. Łojasiewicz, Wstęp do teorii funcji rzeczywistych, PWN,
Warszawa 1976.
- K. Maurin, Analiza, cz. I,II, PWN, Warszawa 1991.
- L. Schwartz, Kurs analizy matematycznej, t.I,II, PWN, Warszawa 1979.
Instytut Matematyki Akademii
Pedagogicznej w Krakowie,
1.10.2005

















