Nastepny dokument:	Wstęp do matematyki z elementami analizy matematycznej
Nadrzędny dokument:	Przedmioty
Poprzedni dokument:	Przedmioty

Geometria

CELE KSZTAŁCENIA

Celem nauczania tego przedmiotu jest powtórzenie i pogłębienie wiadomości słuchaczy z geometrii, które nabywali do końca nauki w szkole średniej, kształtowanie umiejętności rozwiązywania zadań (też problemowych) z geometrii płaskiej i przestrzennej (syntetycznej i analitycznej).

TREŚCI NAUCZANIA

1. Figury elementarne (płaskie i przestrzenne) i ich podstawowe własności

Figury wypukłe. Pojęcie kąta płaskiego, kąta dwuściennego, kąta liniowego kąta dwuściennego. Kąty przyległe, kąty wierzchołkowe. Kąt między prostymi, prostą a płaszczyzną. Proste prostopadłe, prosta prostopadła do płaszczyzny, płaszczyzny prostopadłe. Odległość geometryczna punktów, punktu od figury, prostych równoległych, płaszczyzn równoległych, prostych skośnych, symetralna odcinka i dwusieczna kąta. Kula, sfera (koło, okrąg). Figury ograniczone, nieograniczone, otwarte, domknięte, wnętrze, zewnętrze, brzeg figury. Wzajemne położenie prostej i sfery (okrągu), płaszczyzny i sfery, dwóch sfer (okręgów tej samej płaszczyzny). Kąty środkowe i wpisane w okrąg. Łamana, łamana zwyczajna, wielokąty. Kąty wewnętrzne i zewnętrzne wielokąta, przekątne wielokąta. Trójkąt; związki między bokami i kątami, symetralne boków trójkąta, środkowe, dwusieczne kątów wewnętrznych, wysokości trójkąta i twierdzenia z nimi związane - różne sposoby ich dowodzenia. Twierdzenie Cevy i wnioski z tego twierdzenia. Czworokąty wpisane w okrąg i opisane na okręgu. Twierdzenie Ptolemeusza. Wielokąty foremne. Wielościany; graniastosłupy i ostrosłupy, siatki wielościanów. Twierdzenie Eulera dla wielościanów wypukłych, wielościany foremne. Bryły obrotowe.

2. Metoda analityczna

Opisywanie figur równaniami, nierównościami, układami równań lub nierówności. Rozwiązywanie zadań, w szczególności dowodzenie twierdzeń metodami geometrii analitycznej.

3. Przekształcenia geometryczne

• Izometrie na płaszczyźnie i w przestrzeni; podstawowe własności i niezmienniki izometrii, symetrie: osiowa, środkowa, płaszczyznowa. Generowanie dowolnej izometrii symetriami. Przystawanie figur; cechy przystawania figur (w szczególności cechy przystawania trójkątów). Środek symetrii, oś symetrii, płaszczyzna symetrii figury. Wektory zaczepione i swobodne; równość wektorów, działania na wektorach. Translacje i ich związek z symetriami, własności translacji. Kąt skierowany, równość kątów skierowanych, działania na kątach skierowanych, orientacja płaszczyzny. Obrót wokół punktu na płaszczyźnie i wokół prostej w przestrzeni o dany kąt skierowany, składanie obrotów. Izometrie parzyste i nieparzyste. Izometrie własne figur (m.in. prostej, okręgu, trójkąta równobocznego, kwadratu, czworościanu foremnego).
• Jednokładność; podstawowe własności i niezmienniki jednokładności, składanie jednokładności o tym samym środku i różnych środkach, przykłady figur jednokładnych.
• Podobieństwa; własności podobieństw, niezmienniki, rozkład podobieństwa na jednokładność i izometrię, figury podobne; przykłady figur podobnych, cechy podobieństwa figur (w tym również trójkątów). Związki miarowe w trójkącie prostokątnym, twierdzenie Pitagorasa.
• Rzut równoległy płaszczyzny na prostą tej płaszczyzny. Rzut równoległy w przestrzeni. Własności niezmiennicze figur w rzucie równoległym, twierdzenie Talesa, twierdzenie o dwusiecznej kąta wewnętrznego i zewnętrznego w trójkącie, ,,złoty" podział odcinka.

4. Konstrukcje geometryczne na płaszczyźnie

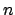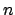Zadanie konstrukcyjne i jego rozwiązanie (analiza, opis konstrukcji, dowód poprawności, dyskusja istnienia i ilości rozwiązań). Przegląd wybranych konstrukcji (np. okrąg opisany na trójkącie, okrąg wpisany w trójkąt, styczna do okręgu przechodząca przez dany punkt, $n$-kąt foremny dla $n$ = 3, 6, 4, 8, 5, 10, 15. Metody rozwiązywania zadań konstrukcyjnych; w szczególności wykorzystanie przekształceń geometrycznych do rozwiązywania zadań konstrukcyjnych. Problem konstruowalności wielokątów foremnych; twierdzenie Gaussa.

5. Mierzenie figur geometrycznych

Miara; twierdzenie o istnieniu miary odcinków przy zadanej jednostce, twierdzenie o zmianie jednostki, iloraz odcinków. Miara kątów (stopniowa i łukowa i związek między nimi). Pola figur płaskich: konstrukcja miary polowej w sensie Jordana; miara wewnętrzna i zewnętrzna figur ograniczonych; warunek wystarczający na istnienie miary polowej figur; twierdzenie o zmianie jednostki pola i polach figur podobnych; pole prostokąta, trójkąta, pole koła i innych figur geometrycznych.

LITERATURA

1. R. Doman, Wykłady z geometrii elementarnej, Wydawnictwo Naukowe UAM, Poznań, 2001.
2. M. Łuczyński, Z. Opial, O konstrukcjach trójkątów, PZWS, Warszawa, 1964.
3. K. Kłaczkow, M. Kurczak, E. Zwida, Matematyka. Podręcznik do liceów i techników, kl. I, II, III.
4. Z. Krygowska, J. Moroszkowa, Geometria dla klasy I Liceum Ogólnokształcącego, PZWS, Warszawa 1967.
5. Z. Krygowska, J. Moroszkowa, Geometria dla klasy II Liceum Ogólnokształcącego, PZWS, Warszawa 1969.
6. Z. Krygowska, G. Treliński, Geometria dla klasy IV Liceum Ogólnokształcącego i Technikum.
7. S. Serafin, G. Treliński, Zbiór zadań z matematyki elementarnej. Geometria, PWN, Warszawa 1976.

Nastepny dokument:	Wstęp do matematyki z elementami analizy matematycznej
Nadrzędny dokument:	Przedmioty
Poprzedni dokument:	Przedmioty