Celem przedmiotu jest z jednej strony pogłębienie i usystematyzowanie
wiadomości z logiki matematycznej i teorii zbiorów i funkcji (aby
przygotować słuchacza do studiowania innych przedmiotów), a z drugiej strony
gruntowne przyswojenie przez słuchaczy podstaw analizy matematycznej
koniecznych w nauczaniu szkolnym.
- Rachunek zdań. Zmienne zdaniowe i funktory zdaniotwórcze. Prawa
(tautologie) rachunku zdań. Formy zdaniowe. Równania i nierówności jako
formy zdaniowe. Kwantyfikatory. Prawa rachunku kwantyfikatorów.
- Zbiory, relacje i funkcje. Algebra zbiorów. Iloczyn kartezjański
zbiorów. Relacje. Funkcje jako relacje, obraz i przeciwobraz zbioru.
Funkcje różnowartościowe. Funkcja odwrotna. Funkcja złożona.
- Relacja porządkująca i równoważnościowa. Zbiory uporządkowane.
Relacja równoważnościowa i zasada abstrakcji. Zastosowanie relacji
równoważnościowych do definiowania pojęć i konstrukcji zbiorów
liczbowych.
- Zasada indukcji matematycznej.
- Ciągi i ich własności. Pojęcie ciągu i podciągu. Ciągi monotoniczne i
ograniczone. Ciągi definiowane rekurencyjnie. Ciąg arytmetyczny i
geometryczny. Granica ciągu. Granice specjalne. Liczba
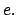
- Szeregi liczbowe. Pojęcie szeregu. Szereg geometryczny i jego suma.
Ważniejsze kryteria zbieżności szeregu.
- Funkcje liczbo-liczbowe. Zbiór
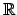 liczb rzeczywistych. Funkcje
określone w podzbiorach
liczb rzeczywistych. Funkcje
określone w podzbiorach
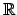 o wartościach w
o wartościach w
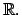 Dziedzina funkcji. Wykres
funkcji. Miejsca zerowe funkcji. Funkcje parzyste i nieparzyste.
Funkcje okresowe. Przekształcanie wykresu funkcji.
Dziedzina funkcji. Wykres
funkcji. Miejsca zerowe funkcji. Funkcje parzyste i nieparzyste.
Funkcje okresowe. Przekształcanie wykresu funkcji.
- Funkcje elementarne. Funkcja liniowa i kwadratowa, wielomiany. Funkcja
homograficzna, funkcje wymierne. Potęga o wykładniku rzeczywistym.
Funkcja potęgowa. Funkcja wykładnicza i logarytmiczna. Funkcje
trygonometryczne i cyklometryczne. Równania i nierówności: liniowe,
kwadratowe, wielomianowe, wymierne, wykładnicze, logarytmiczne i
trygonometryczne.
- Granica i ciągłość funkcji. Definicja Heine'go i Cauchy'go
granicy funkcji, ich równoważność. Granice jednostronne. Asymptoty
funkcji. Ciągłość funkcji. Lokalne i globalne własności funkcji
ciągłych. Ciągłość funkcji elementarnych.
- Pochodna funkcji. Definicja pochodnej, interpretacja
geometryczna, fizyczna i ekonomiczna pochodnej. Definicja stycznej do
wykresu funkcji. Pochodne funkcji elementarnych. Pochodne wyższych
rzędów.
- Twierdzenia o wartości średniej. Twierdzenia: Rolle'a, Lagrange'a
i Taylora o wartości średniej. Zastosowanie tych twierdzeń do badania
funkcji (monotoniczność, ekstrema lokalne, wypukłość i punkty
przegięcia) i dowodów niektórych nierówności. Reguła de l' Hospitala.
- Całka nieoznaczona. Funkcja pierwotna i jej własności. Całkowanie
niektórych funkcji.
- Całka oznaczona. Sumy całkowe Riemanna. Całka oznaczona Riemanna
i jej własności. Związek miary Jordana z całką Riemanna. Geometryczne
i fizyczne zastosowania całek Riemanna. Całka Lebesgue'a
(informacyjnie) - porównanie z całką Riemanna.
- A. Birkholz, Analiza matematyczna dla nauczycieli, PWN,
Warszawa 1977.
- A. Chronowski, Z. Powązka, Pochodna funkcji, Wydawnictwo ,,Dla
Szkoły", Bielsko-Biała 2000.
- H. Kąkol, Z. Powązka, Pojącie funkcji, Wydawnictwo ,,Dla
Szkoły", Bielsko-Biała, 1994 (cz. I), 1995 (cz. II).
- W. Krysicki, L. Włodarski, Analiza matematyczna w zadaniach, cz.
I, PWN, Warszawa 1994.
- Z. Moszner, O teorii relacji, PZWS, Warszawa 1967.
- J. Musielak, Wstęp do matematyki, PWN, Warszawa 1970.
- H. i J. Musielakowie, Analiza matematyczna, Wydawnictwo Naukowe
UAM, Poznań, 1993 Tom I (cz. 1), Poznań 2000 Tom I (cz. 2).
Instytut Matematyki Akademii
Pedagogicznej w Krakowie,
28.09.2006

















