Celem nauczania jest przedstawienie podstawowych pojęć i rezultatów algebry
w stopniu wystarczającym do algebraicznego opisu fragmentów
matematyki szkolnej i teorii matematycznych poznawanych w
czasie studiów.
| SEMESTR 4 | TREŚCI NAUCZANIA |
- Grupy, podgrupy. Twierdzenia Lagrange'a i Cayley'a. Dzielniki normalne,
kongruencje, grupy ilorazowe. Podstawowe twierdzenie o
homomorfiźmie grup. Grupy cykliczne, grupy skończenie generowane. Grupy
abelowe, twierdzenie o strukturze grup abelowych skończenie
generowanych. Suma
prosta grup. Grupy
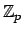 . Komutanty grup. Grupy rozwiązalne.
Grupy proste. Grupy symetryczne
. Komutanty grup. Grupy rozwiązalne.
Grupy proste. Grupy symetryczne 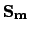 i grupy alternujące.
Rozwiązalność grup
i grupy alternujące.
Rozwiązalność grup 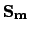 .
.
- Ideały, kongruencje, pierścienie ilorazowe. Homomorfizmy
pierścieni i ich jądra. Podstawowe twierdzenie o
homomorfiźmie pierścieni. Ideały pierwsze i maksymalne.
Ciało ułamków pierścienia całkowitego. Liczby naturalne,
całkowite, wymierne. Charakterystyka pierścienia.
Pierścienie wielomianów, macierzy i pierścienie szeregów potęgowych.
Wielomiany symetryczne.
- Relacja podzielności, elementy stowarzyszone, elementy
nierozkładalne i pierwsze. Pierścienie z rozkładem i z jednoznacznością
rozkładu. Największy wspólny dzielnik,
najmniejsza wspólna wielokrotność. Ideały główne, pierścienie główne.
Pierścienie noetherowskie, pierścienie Euklidesa. Teoria podzielności w
pierścieniu wielomianów. Twierdzenie Gaussa, wymierne pierwiastki wielomianu,
kryterium Eisensteina. Pierścień
![$\mbox{$\mathbb{Z}$}[\sqrt{d}]$](img16.gif) .
.
| SEMESTR 5 | TREŚCI NAUCZANIA |
- Ciała skończone. Elementy algebraiczne i przestępne. Rozszerzenia proste,
skończone i algebraiczne. Ciało liczb rzeczywistych i ciało liczb
zespolonych. Domknięcie algebraiczne. Ciało
rozkładu wielomianów. Element pierwotny
rozszerzenia. Automorfizmy ciał. Grupa Galois, rozszerzenie
Galois. Zasadnicze twierdzenie algebry.
- Rozszerzenia pierwiastnikowe i konstruowalne. Ciało liczb
konstruowalnych. Rozwiązywanie równań przez
pierwiastniki i zastosowanie do konstrukcji geometrycznych.
- Elementy teorii liczb (kongruencje i
ich rozwiązywanie, cechy podzielności, twierdzenia
Lagrange'a, Wilsona i Fermata, przykłady zastosowań teorii pierścieni z
jednoznacznością rozkładu do rozwiązywania równań diofantycznych).
- Grupy, pierścienie i ciała uporządkowane, własność
Archimedesa. Zastosowania do struktur liczbowych.
- A. Białynicki-Birula, Algebra, PWN, Warszawa 1971.
- A. Białynicki-Birula, Zarys algebry, PWN, Warszawa 1987.
- J. Browkin, Teoria ciał, PWN, Warszawa 1978.
- M. Bryński, J. Jurkiewicz, Zbiór zadań z algebry, Warszawa 1978.
- A. Chronowski, Podstawy arytmetyki szkolnej cz. 1 i 2, Błękitna
Matematyka, Wydawnictwo ,,Kleks'', Bielsko-Biała 1999.
- B. Gleichgewicht, Algebra, Podręcznik dla kierunków
nauczycielskich studiów matematycznych, PWN, Warszawa 1983.
- N. Koblitz, Wykłady z teorii liczb i kryptografiia, WNT,
Warszawa 1995.
- A.I. Kostrykin, Zbiór zadań z algebry, Warszawa 1995.
- S. Lang, Algebra, PWN, Warszawa 1983.
- A. Łomnicki, M. Magdoń, M. Żurek-Etgens, Grupy,
pierścienie, ciała w zadaniach, WN WSP, Kraków 1991.
- Z. Opial, Algebra wyższa, PWN, Warszawa 1974.
- J. Rutkowski, Algebra abstrakcyjna w zadaniach, PWN,
Warszawa 2000.
- K. Szymiczek, Zbiór zadań z teorii grup, PWN, Warszawa
1989.
Instytut Matematyki Akademii
Pedagogicznej w Krakowie,
15.06.2003








